By the end of year 7
Number and algebra | Geometry and measurement | Statistics
The following problems and descriptions of student thinking exemplify what is required to meet this standard.
Number and algebra
In contexts that require them to solve problems or model situations, students will be able to:
- apply additive and multiplicative strategies flexibly to whole numbers, ratios, and equivalent fractions (including percentages)
- apply additive strategies to decimals
- balance positive and negative amounts
-
find and represent relationships in spatial and number patterns, using:
- tables and graphs
- general rules for linear relationships.
During this school year, 'number' should be the focus of 40–60 percent of mathematics teaching time.
Example 1
There are 6 baskets and 24 muffins in each basket.
How many muffins are there altogether?
The student uses an efficient multiplicative strategy to solve the problem mentally. This might involve drawing on their knowledge of place value (for example, 6 x 20 + 6 x 4), working with tidy numbers (for example, 6 x 25 – 6 x 1), or doubling and halving (for example, 6 x 24 = 12 x 12).
If the student uses repeated addition or doubling (for example, 24 + 24 = 48, 48 + 24 = 72 ...), they do not meet the expectation. If they use a vertical algorithm to solve the problem, they must explain the place value partitioning involved.
Source: Numeracy Development Projects, Book 2: The diagnostic interview, p. 41.
Example 2
Tama has 4.95 litres of petrol in one can and 7.5 litres in the other can.
How much petrol does he have altogether?
The student demonstrates their understanding of decimal place value when combining the amounts.
Appropriate strategies include using compensation (for example, 4.95 + 7.5 = 4.45 + 8 = 12.45), working with tidy numbers (for example, 5 + 7.5 = 12.5, so 4.95 + 7.5 = 12.45), or drawing on knowledge of place value (for example, 4 + 7 = 11 and 0.9 + 0.5 = 1.4, so 4.95 + 7.5 = 12.45).
If the student combines place values inappropriately (for example, 4.95 + 7.5 = 11.100 or 4.95 + 7.5 = 11.145), they do not meet the expectation. If they use a vertical algorithm to solve the problem, they must explain the place value partitioning involved.
Example 3
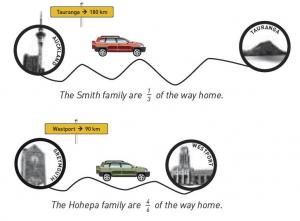
Show the student the following illustration.
The Smith family and the Hohepa family are both driving home from their holidays.
Which family has travelled the greatest distance?
The student shows that they understand that the value of a fraction of an amount depends on both the fraction and the amount. They do so by calculating the distance each family has travelled, using multiplication and division (for example, 1/3 of 180 = 180 ÷ 3 = 60). If the student recognises that 4/6 is equivalent to 2/3 , the second calculation is considerably simplified (2/3 of 90 = 90 ÷ 3 x 2 = 60).
If the student bases their answer on just the amounts (for example, 'The Smiths because 180 is greater than 90') or just the fractions (for example, 'The Hohepas because 4/6 is greater than 1/3'), they do not meet the expectation. If they notice and use the doubling and halving relationship (1/3 of 180 = 4/6 of 90 because 4/6 = 2 x 1/3 ), they exceed the expectation.
Example 4
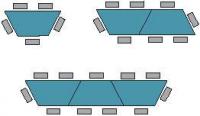
Show students the following illustration.
Funky Furniture sells tables that can be joined together for large meetings. Tables and chairs are set up this way.
If a line of 24 tables is set out like this, how many chairs will be needed? Can you give a rule for the number of chairs needed for any given number of tables?
The student recognises that 3 extra chairs are needed for each extra table. They apply multiplicative thinking to calculate the number of chairs needed for 24 tables (for example, '21 more tables x 3 = 63 extra chairs, 11 + 63 = 74 chairs altogether' or '5 chairs for table one + 23 tables x 3 = 74 chairs altogether').
The student devises a general rule for any number of tables (for example, 'Multiply the number of tables by 3 and add 2'). If they give an algebraic equation (for example, 'If x = tables and y = chairs, then y = 3x + 2'), they exceed the expectation.
Source: adapted from PAT, Test 4, Item 30, © NZCER 2007.
Return to top
Geometry and measurement
In contexts that require them to solve problems or model situations, students will be able to:
- measure time and the attributes of objects, using metric and other standard measures
- make simple conversions between units, using whole numbers
- use side or edge lengths to find the perimeters and areas of rectangles and parallelograms and the volumes of cuboids, given whole-number dimensions
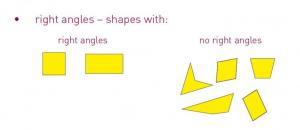
- sort two- and three-dimensional shapes into classes, defining properties and justifying the decisions made
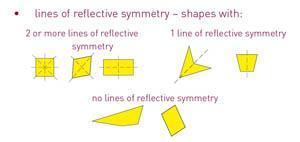
- identify and describe the transformations that have produced given shapes or patterns
- create or identify nets for rectangular prisms and other simple solids
- draw plan, front, side, and perspective views of objects
- describe locations and give directions, using grid references, simple scales, turns, and points of the compass.
Example 5
Provide the students with coins and kitchen scales, as required for 1. below.
The students at Springfield School made a coin trail using 20-cent coins to raise money for Daffodil Day.
- The length of the coin trail was 21 000 millimetres. What was its length in centimetres? What was it in metres?
- Here are 100 twenty-cent coins. Use the kitchen scales to find their combined weight. Using your answer, what would 1000 twenty-cent coins weigh? What would 10 twenty-cent coins weigh?
For 1., the student reads the scales accurately to give the combined weight as 400 grams. They use their knowledge of place value, metric measures, and multiplicative strategies to correctly answer all other questions – for example, for 1., 'There are 10 millimetres in a centimetre, so 21 000 mm = 2100 cm; there are 1000 millimetres in a metre, so 21 000 mm = 21 m'; for 2., '1000 coins must weigh 10 times 400 grams, which is 4000 grams or 4 kilograms; 10 coins must weigh one-tenth of 400 grams, which is 40 grams.'
Source: adapted from 'Coin trail' (MS2161) in the Assessment resource banks
Example 6
Give the student the following collection of shapes.
- What is a common property of all these shapes?
Identify a property that some of the shapes have and sort all the shapes into groups by that property.
For 1., the student identifies at least one property that is common to all the shapes – for example, they all have 4 sides, 4 corners (vertices), or straight sides (that is, they are all polygons).
For 2., the student identifies an appropriate property and sorts the shapes into classes by that property – for example, whether each shape has:
Example 7
Provide square grid paper, a ruler, and a protractor. Show the student the following illustration.
Draw a net for each of these solids. You may try each net by cutting it out and folding it to make the solid. It may take several attempts to get it right.
The student creates nets for the four solids by visualising the shape and size of each face and how the faces fit together. They describe the similarities and differences between the solids (for example, rectangular faces, triangular versus square ends) and use this information to help construct the nets.
The student must precisely measure the dimensions of the faces and orient them so that, when brought together, they form an accurate model of the original solid. It is acceptable to support the student by suggesting that, when drawing a net, they orient the solid’s faces on horizontal and vertical axes.
Source: adapted from Figure it out – Geometry, level 3, p. 11.
Return to top
Statistics
In contexts that require them to solve problems or model situations, students will be able to:
-
investigate summary, comparison, and relationship questions by using the statistical enquiry cycle:
- gather or access multivariate category and measurement data
- sort data and display it in multiple ways, identifying patterns and variations
- interpret results in context, accepting that samples vary and have no effect on one another
- order the likelihoods of outcomes for situations involving chance, checking for consistency between experimental results and models of all possible outcomes.
Example 8
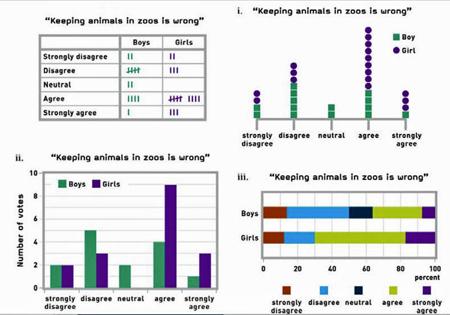
Show the student the illustrations below.
Here are the results from a class opinion poll, recorded on a tally chart and displayed in three different graphs.
Look at the data gathered in the poll. Suggest some different types of questions that could be answered from the data, for example, summary questions like 'How many girls disagree that keeping animals in zoos is wrong?' or comparison questions like 'Do more boys or girls agree that keeping animals in zoos is wrong?'
Now write down some 'I wonder' questions about people’s opinions on topics of interest to you, your friends, or your family. Work with one or two other students to use the statistical enquiry cycle to investigate one or more of your questions.
Source: Census at school, Data detective
Make sure your records of your investigation clearly show how you gathered, sorted, and displayed your data and what you interpreted from it.
The student should move through all stages of the enquiry cycle. (Note that at times their findings may require them to go back to previous stages.) They may phrase the problem as a summary question (for example, 'What do people feel about banning fireworks?'), a comparison question (for example, 'Do boys and girls feel differently about banning fireworks?'), or a relationship question (for example, 'Is there a link between people’s ages and how they feel about banning fireworks?').
In planning the investigation, the student should consider what data they need to answer the question and how they will collect and manage this data. This may involve finding a way of 'measuring' aspects such as people’s feelings or attitudes.
Having collected the data, the student should consider how they will sort and display it to provide answers to their question. They should use tables and graphs and may access a computer program to create their displays. Their displays should be appropriate for the type of data, for example, bar or pie charts for category data, stem-and-leaf plots or dot plots for whole-number data, histograms for measurement data, and line graphs for time-series data. The student may use multiple displays to identify patterns and variations in the data.
The student should interpret and report their results in context, using features of their displays to support their findings and acknowledging that different samples might give different results.
Sources: adapted from Figure it out – Statistics, levels 3–4 (rev), p. 6.
Example 9
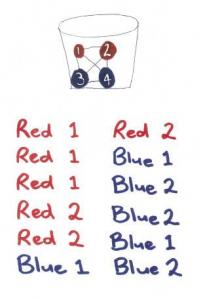
Show the student a bucket containing 2 red balls and 2 blue balls.
What are all the possible outcomes when you randomly draw 2 balls from the bucket?
What is the probability of getting 2 red balls?
How many times would you expect to get 2 red balls in 60 draws?
Now trial the situation by drawing 2 balls 60 times and recording your results on a tally chart. Then summarise your results on a frequency table, like this:
How do your results compare with your prediction of how often you’d draw 2 red balls? Do the results make you change your prediction?
If you repeated the trial with 60 draws, how many times would you get 2 red balls?
The student creates a model of all the possible outcomes when 2 balls are removed from the bucket. From this, they identify that 2 red balls is one of 6 possible outcomes, and they predict that this outcome should occur about 10 times in 60 draws.
The student accepts that the experimental results are consistent with their prediction despite any variation from 10 red-red occurrences. They predict that in a second trial, 2 red balls will be drawn approximately 10 times. They also recognise that the results are unlikely to be identical to those in the first trial, that is, they accept the variability and independence of samples.
Source: adapted from The New Zealand Curriculum exemplars – Statistics: Probability, level 3ii.
Published on: 15 Oct 2009
Return to top